Fuzzy Patches in the Sky: The Proof of the Pudding!

“And God said, “Let there be lights in the vault of the sky to separate the day from the night, and let them serve as signs to mark sacred times, and days and years, ¹⁵ and let them be lights in the vault of the sky to give light on the earth.” And it was so. ¹⁶ God made two great lights—the greater light to govern the day and the lesser light to govern the night. He also made the stars. ¹⁷ God set them in the vault of the sky to give light on the earth, ¹⁸ to govern the day and the night, and to separate light from darkness. And God saw that it was good. ¹⁹ And there was evening, and there was morning—the fourth day”

-  - Genesis, Chapter 14.

In previous blogs in this series, trying to reconcile the creation story of Genesis with the limited speed of light left us scratching our heads.  According to Genesis, God created the stars to light up the night on the fourth day of the seven days that He took to create the universe. The purpose of creating the stars, as you just read in Chapter 14, was to provide light during the night.  In a single day, though, the light generated by creating even the nearest star, Alpha Centauri, would cover only about 1/1500 of the distance to the Earth, so even Alpha Centauri wouldn’t have appeared in the sky for four years after the fourth day.  All the other stars in the sky would have taken longer – some over a thousand years longer – to add their luster.  If God’s purpose in creating the stars was to light up the night on the Fourth Day, it is difficult to understand why He placed them much too far away to achieve His goal. 

But we also discovered that the stars aren’t the only sources of light in the night sky.  Take the fuzzy patch of light in the Southern Hemisphere known as the Small Magellanic Cloud (SMC). At the beginning of the last century, astronomers were able to use Henrietta Leavitt’s discovery of Cepheid Variables in the SMC to determine, for the first time, that the SMC lies at least 30,000 light years away (close to 200,000 light years distant by modern calculations).  In a single day, therefore, light from the SMC covers only about one seventy-three millionth of the distance to the Earth.  If the SMC was created, along with the rest of the Universe, some 6,000 years ago, there is no way the cloud would have been visible to Ferdinand Magellan and his band of explorers in the early 1500’s; no way it (and its Cepheids) would have showed up on Henrietta Leavitt’s photographic plates in the first decade of the 20^th century, and no way it would be visible today. We would be completely ignorant of SMC’s presence until about 194,000 A.D., when its light would finally arrive!

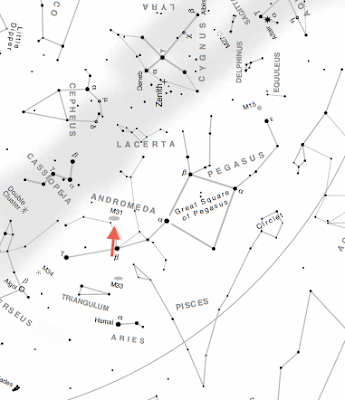
The fact that the SMC (and its neighbor, the Large Magellanic Cloud) has been visible throughout recorded history is proof that the universe is at least 200,000 years old, a far cry from 6,000.  But the story of Cepheid Variables, and the headaches they create for Genesis, doesn’t end with the SMC; not by a long shot.  Almost 600 years before Ferdinand Magellan set out on his voyage of discovery and saw the Magellanic clouds that would come to bear his name, a Persian astronomer named Abd al-Rahman al-Sufi left a diagram suggesting that he had noticed the existence of another mysterious patch of light, this one in the constellation Andromeda, the maiden.  Shown in the left figure below, the diagram includes a maiden, Andromeda, a fish, and a mysterious collection of dots just to the right of the fish’s nose.  This is the first record of anybody actually noticing the mysterious smudge of light that is now known as the Andromeda Galaxy.  If you have clear skies tonight, and live in an area with minimal light pollution, this smudge will be visible to you, too.  As shown in the figure below and to the right, find the Great Square of Pegasus in the northwest about an hour after sundown.  Count two stars over and then look up a little to the location indicated by the red arrow.  The fuzzy patch you see is the focus of today’s blog.

By the beginning of the 20^th century, centuries of observations with previous generations of telescopes had revealed many other wispy patches just like the Andromeda Galaxy.  With no way to determine their distances, though, these “nebula” had become the focus of a battle royal in astronomical circles: Were they some sort of mysterious agglomerations of matter inside our own galaxy, solar systems in the making perhaps, or were they other galaxies, far further away than our Milky Way, but otherwise resembling our own?

Solving this thorny question would fall to no other than Edwin Hubble, the famous American astronomer that the Hubble Space Telescope is named after (we’ll see presently one of the primary reasons why that naming was so appropriate).  In the 1920’s, Hubble was fortunate enough to be one of the first astronomers to utilize a marvelous new telescope on Mount Wilson in Southern California, the first in the world to have a primary mirror more than 100 inches (8 feet!) in diameter. It was Hubble who realized that this telescope would be powerful enough to actually resolve the brightest stars in the Andromeda galaxy.  Luckily, Cepheid Variables are supergiant stars that have moved off the “main sequence” – a concept I’ll be glad to clarify in the comment section, if anyone’s interested – and have swollen to a gigantic size as a result.  Even the dimmest Cepheids outshine the Sun by a considerable margin, and the very brightest, those with the longest periods, are 100,000 times as bright. Hubble knew that if he could find Cepheids in the Andromeda Nebula, he could measure the distance to it, and put an end to the raging debate once and for all.

The figure below is an example of one of the photographs of the Andromeda “nebula” taken by Hubble with his new gigantic telescope.  And lo and behold, as you can see from the label in the center, Hubble was successful in his quest; some of the individual stars in these photos did indeed demonstrate the periodic brightening and dimming cycles that marked them as Cepheids!   Carrying out the usual computations based on comparing the brightness of these Cepheids as measured in the photographs against their true intrinsic brightness as determined by their location along the period/luminosity function, Hubble announced his determination to the world: The Andromeda “Nebula” was actually 600,000 light years away!  At that enormous distance, it couldn’t be a part of our galaxy, but instead must be a galaxy in it’s own right, a magnificent “island universe” like the Milky Way containing billions and billions of stars.

The mystery of the nebulas was solved, and in one magnificent step, Edwin Hubble was able to provide humanity with a true perspective on the size of the cosmos.  The Earth wasn’t the center of the universe; it was located in a spur of a spiral arm of a galaxy named the Milky Way, an insignificant spec of the universe surrounded by untold numbers of other galaxies in every direction, all at unimaginable distances from our own. The modern value for the distance to the Andromeda galaxy is 2.5 million light years.

The fact that you can go out tonight and actually SEE the Andromeda galaxy, when its light takes a full two and a half million years to reach us, starts to reveal just how completely nonsensical the timeline for the creation of the universe in Genesis really is.   And the fun doesn’t stop there.  Hubble was able to resolve Cepheids in many other galaxies, some as far as 10 million light years distant. As he analyzed the light from the unimaginably distant stars in these galaxies, he noticed another quality of their light that would profoundly change our understanding of the history of the universe and how it all began.

But that’s a topic for another blog!

The Cloud in God's Eye

Henrietta Leavitt published her finding that the intrinsic (the “real”) brightness of a Cepheid variable was strongly related to its period (the duration of its fluctuation cycle) in 1912.   It didn’t take long for astronomers to realize the important implications of this relation.  If they could just figure out the actual distance to even one Cepheid (obviously, that would have to be a cepheid closer to our neck of the woods than the collection Henrietta discovered in the Small Magellanic Cloud), they could calculate the distance to the SMC using the inverse square law!

How?  Remember a couple of blogs ago, when I explained the inverse square law using a pair of identical candles?  The two conditions needed to made the law work were, one, you had to know the actual distance to one member of the pair (in my example, it was the distance to the nearer candle), and two, both candles had to be identical, so they would shine equally brightly if placed at the same distance from you.  That way, after your friend put the second candle some unknown distance away, you could be confident that the only source of their (now) differing brightness was their unequal distance.

With those two factors in mind, consider our old friend Delta Cep.  Long before Henrietta Leavitt turned her attention to the Cepheids in the SMC, Delta Cep’s period had been determined to be 5.4 days, and its apparent magnitude (brightness) had been pegged at 4.3 at the dimmest point in its cycle (by the way, that’s about mid-way between the brightest and dimmest stars visible to the naked eye.  You can find Delta Cep yourself in the circumpolar constellation Cepheus if you consult a star chart and live in an area with reasonably dark skies).  Today, we know from parallax measurements with the Hubble Space Telescope that Delta Cep is about 891 light years away.  Courtesy of Leavitt’s discovery, any Cepheid whose period is equal to Delta Cep’s has the same intrinsic brightness; a pair of such stars would be like identical candles.  If an astronomer from 1912 had known Delta Cep’s distance, then using the Period-Luminosity functions from Leavitt’s SMC sample, he or she could have easily calculated how bright a Cepheid with Delta Cep’s period would be if it was located in the SMC (or, if you like, the brightness of Delta Cep itself if it were in the SMC). 

The figure below illustrates how this would have been done.   First, you would have located the point along the X-axis that corresponds to the log of Delta Cep’s 5.4 day period (about the 0.5 point). Then, you’d have drawn a straight line up from the 0.5 point to the lower of the two period-luminosity plots inside the figure (that’s the one that plots the Cepheids in the SMC at the dimmest point in their cycles).  Next, you’d have drawn a horizontal line from the plot across to the Y-axis (the horizontal red line in the figure), and simply read the magnitude where the line intersects that axis.  When I do that, just by eye I get an apparent magnitude of approximately 15.8.

Finally, all the conditions would be met to employ the inverse square law!  The difference between an object of magnitude 15.8 and an object of magnitude 4.3 corresponds to a difference in brightness of 11.5 units along the magnitude scale.  In turn, that difference translates into the fact that Delta Cep’s putative twin in the SMC would be roughly 33,750 times dimmer than the real Delta Cep (the magnitude scale astronomers use to measure brightness is another log-based scale, so it’s highly non-linear).  The inverse square law tells us that brightness falls off with the square of the distance, so Delta Cep’s twin would be about 184 times as far away as Delta Cep (squaring 184 yields approximately 33,750).   Finally, since Delta Cep is itself 891 light years away, its twin (and therefore the SMC itself) must be 184 multiplied by 891, or 164,000 light years distant - a figure within respectable shouting distance of the modern estimate, which is around 210,000 light years.

Of course, I cheated.   Astronomers in 1912 didn’t know the distance to Delta Cep, so they couldn’t compute that actual distance to the SMC.  They would have had to be content with the knowledge that, however far away Delta Cep was, the SMC was some 184 times further away than that.  A pretty strong clue, you’d have to admit, that some of the objects in the night sky were very, very far away, indeed.

But astronomers of the time wanted more: they wanted the actual distance to the SMC! Energized by the prospect, a contemporary of Henrietta Leavitt’s, Earnest Hertzsprung, set out to measure the distances to known Cepheids within our galaxy using several distance-measuring techniques that I won’t get into here.  Although none of these techniques was as accurate as the trigonometric parallax method, Hertzsprung still managed to derive crude distance measurements to not one, but 13 Cepheids. 

Those distances gave Hertzsprung the tools he needed to make a preliminary determination of the distance to the SMC using the method described above.  The value he obtained, 30,000 light years, was far short of the modern value of over 200,000 light years.   But even Hertzsprung’s gross underestimation was large enough to deal another devastating blow to the Biblical story of Creation.  According to literalist biblical scholars, the universe is only about 6000 years old.  Furthermore, according to Genesis, all the sources of light in the night sky were created in a single 24-hour period – the fourth day after God initiated the Creation process (and there are records of peoples in the Southern Hemisphere having seen the SMC as long as thousands of years ago, so it was definitely present in the sky during biblical times).  But if the SMC was created only 6000 years ago, the light from the cloud has not had time to cross more than a small fraction of the distance between it and the Earth, even with Hertzsprung’s gross underestimate. Given our current understanding of the true distance to the SMC, the cloud could not appear in our skies until after 200,000 AD!  That’s so far in the future I can’t even imagine it.

Is there an alternative way to save the biblical story?  In one of the earlier blogs in this series, I considered a rather unlikely account for how the literal account of Creation could be reconciled with the fact that even the nearest stars are so far away that their light takes years to reach the Earth.  On the fourth day of creation, God would have had to place those stars within the confines of our own solar system (so that their light had a chance to make it to the Earth before the fourth night descended), and then He would have had to whisk them out to their current positions.  While God would have had to hurry some of these stars along pretty fast – at 26 light years away, a star like Vega would take longer than 6000 years to reach its present position even if it was moving as fast as our fastest jetliners – our spacecraft travel much faster than that, so I don’t think God would have found it a problem. 

But even this rather far-fetched account would fail miserably for the Small Magellanic Cloud.  6000 years is not nearly enough time to transport the SMC even 30,000 light years away unless God was moving all the stars in the cloud far faster than the speed of light!  Not only would that violate all known laws of physics, but it would once again have rendered the Small Magellanic Cloud invisible; its light could not reach us if it was moving away at more than the speed that light travels!

Unfortunately for those who believe in the literal interpretation of Genesis, we’re not finished with the biblical devastation wrought by Cepheid variables.  In the next installment, we’ll tackle some Cepheid-fueled discoveries of an astronomer named Edwin Hubble.  You may have heard of him, or at least of the telescope named after him.

You'll love it at Leavitt's!

By the beginning of the 20^th century, progress in determining the distances to the stars had slowed to a crawl.  The trigonometric parallax method had pretty much pooped out.  Evidence was growing that the stars vary greatly in absolute (intrinsic) brightness, precluding any direct application of the inverse square law.

Fortunately, it is always darkest just before the dawn.  The combination of two advances, one technological and one scientific, was about to provide astronomers with a new and very powerful distance measurement tool.  The technological development was the newly acquired capability to take photographs of telescopic images.  Among other benefits, “astrophotography” would take much of the guesswork out of determining the precise position of a star relative to other stars in its immediate vicinity, breathing new life the trigonometric parallax method and revealing the distances to many additional stars.  Meanwhile, the scientific discovery in question built on a much earlier discovery, made soon after Galileo first turned his telescope to the heavens, that some stars fluctuate in brightness on a fixed, predictable schedule, like Old Faithful. 

Here’s the story.  In 1794, a young English astronomer named John Goodricke identified a distinct subclass of these “variable” stars that would eventually be called “Cepheid” variables.  Although Goodricke had no way of knowing it at the time, Cepheids are giant yellow stars, much brighter and more massive than the Sun.  In addition to being large and luminous, Cepheids display a very distinct fluctuation pattern. The figure below this paragraph shows the pattern for “Delta Cephei”, (or “Delta Cep” for short), one of the few Cepheids actually visible to the naked eye (the North Star, Polaris, is another).  Like all Cepheids, Delta Cep brightens quickly, dims more slowly, and then brightens quickly again, yielding a distinctive “shark fin” shape to the plot of the star’s change in brightness over time (if anyone is interested in why Cepheids behave this way, I’ll be happy to explain it in the comment section). 

Delta Cep fluctuates on a very regular schedule, completing one full cycle every 5.4 days; this is known as Delta Cep’s period.  In common with Delta Cep, all Cepheids fluctuate on very regular schedules.  However, different Cepheids have very different fluctuation periods that range from about one day (for the shortest period Cepheids) to over four months (for the longest).  In the figure below, I show the fluctuation periods for three actual Cepheids that range from a single day to over thirty days.  As you can plainly see, the characteristic “shark fin” shape is present even for the longest period Cepheid, just greatly stretched out in time.

Regardless of their fluctuation period, Cepheids are quite uncommon.  By 1900, only about 30 were known, none close enough to measure a parallax angle and determine its distance.   Back in 1891, however, Harvard College had deployed a 24-inch telescope on a mountaintop in Peru – the first large aperture telescope to be deployed in the Southern Hemisphere.  From 1893 to 1906, this instrument was used to take hundreds of photographs of the Small Magellanic Cloud (hereafter, the “SMC”), a prominent southern sky object named after Ferdinand Magellan, whose crew brought it to the attention of Europeans following their around-the-world voyage in 1519.  As shown in the left-hand photograph below, the SMC looks like a small fuzzy patch to the naked eye. The right-hand image, taken through a telescope, reveals the “cloud” for what it really is: a “dwarf galaxy” containing many millions of stars! 

The telescope in Peru was big enough to resolve the SMC into individual stars.   Exploiting this fact, in 1905 an extremely diligent Harvard astronomer named Henrietta Leavitt began a long-term project to scrutinize the SMC photographs in order to identify variable stars.  After several years of painstaking effort, Leavitt found about a thousand variables, 25 of which pulsed with the distinctive shark-tooth shape that marked them as Cepheids. The shortest-period member of the 25 had a fluctuation period of about one day; the longest-period member, about 128 days.

Next, Henrietta proceeded to measure the apparent (observed) brightness of each SMC Cepheid right at the top and the bottom of their fluctuation cycles (i.e., at the brightest and dimmest points of their respective cycles). The range turned out to be quite substantial, with the brightest member of the 25 being thousands of times more luminous than the dimmest.   Henrietta surmised, correctly as it turned out, that the distance to the SMC was so great that any further differences in distance between her Cepheids and the Earth must be quite inconsequential; to all intents and purposes, they were equally far away.  In turn, this meant that the large differences in apparent brightness among the Cepheids in her sample had to reflect actual differences in their “real” or intrinsic brightness – as opposed to an artifact of their being at different distances from Earth.

Henrietta’s finding that Cepheids differ greatly in intrinsic brightness gave tremendous importance to her next discovery, which came about when she plotted the fluctuation period of each of the 25 Cepheids (X axis) against their apparent brightness at both the top and bottom of their fluctuation cycle (Y axis).  I’ve taken the liberty of reproducing the actual plot from Henrietta’s scientific paper on this topic below.   

For both the top and bottom plots, the key thing to notice is the very strong relation between each Cepheid’s period and its intrinsic brightness: the longer the Cepheid’s period, the brighter it is.  This “period-luminosity” relation showed up even more clearly in the next graph, which shows what happened when Henrietta re-plotted the relation after converting each Cepheid’s period to log-linear coordinates (this just means that she took each Cepheid’s period in days and determined to what exponent the number 10 would have to be raised to equal that number.  For example, a Cepheid with a period of exactly 10 days would have a value of “1” in her log coordinate system; a Cepheid with a period of 100 days would have a value of “2”, and so on).  Now, the “period-luminosity” relation was revealed to be so strong that if you fit a straight-line function to the dots, as Leavitt did in the figure, all 25 Cepheids fell very close to the line at both the minimum and maximum points of their brightness cycles.

I’m going to end this blog with an explanation for another aspect of these graphs that might be puzzling.  Although I’ve explained the log scale along the X-axis, you might still be confused on the other (Y) axis by the fact that the numbers (the brightness scale) go from higher at the origin (the bottom) to lower at the top.  This means that the brighter, long-period Cepheids on the right of the period-luminosity function are associated with a lower number on the brightness scale than the dimmer, lower-period Cepheids down and to the left. 

Why is the number lower, when I just finished noting that the longer-period Cepheids on the right side of the graph were brighter than the shorter-period Cepheids on the left?  The blame belongs to the ancient Greeks, who classified all the stars they could see in the night sky according to their perceived importance.  They declared the very brightest stars, like Sirius, of “first”  (“most important”) magnitude.  Stars of the second magnitude were dimmer, and therefore less important, and so on, all the way down to stars of the sixth magnitude, so dim that they were barely visible (and therefore least important).  Later astronomers adopted this magnitude scale, assigning bright stars (like long-period Cepheids) to lower magnitudes than dimmer stars (like short-period Cepheids).  And while we’re on the topic of magnitude, it’s worth noting that the ancient Greeks included only stars in their magnitude scale, not brighter objects like Venus, the Moon, and the Sun.  When later astronomers began to add these objects to the scale, they had to go to smaller (negative) numbers to convey their apparent brightness (that is, the brightness as measured from here on Earth).  For example, when at its most dazzling, Venus shines with an apparent magnitude of -4.5; The Sun shines with an apparent magnitude of about -27.  On the other end of the scale, stars that are way too dim to be seen in anything but telescopes have apparent magnitudes that extend all the way “up” to +30.  As you can see from Henrietta Leavitt’s plots, the Cepheids in the SMC had apparent magnitudes all the way up in the mid teens, though they were far too faint to be seen with the naked eye.  So the rule of thumb is: The lower the magnitude, the brighter the star.

In the next blog, we’ll continue the discussion of Leavitt’s period-luminosity function and what astronomers could do with it. 

Breaking the Inverse Square Law

As we discussed in the last blog (tragically, a full month ago now), it took over a century of dedicated effort on the part of several generations of astronomers before Friedrich Bessel finally succeeded in measuring the distance to a nearby star, 61 Cygni.  Right on his heels, contemporaries of Bessel’s reported similar success with measuring the distance to two additional stars, Alpha Centauri (the closest star of all) and Sirius, the brightest star.  As we discovered, the enormous magnitude of these distances, none less than 25 trillion miles, combined with the finite speed of light, spelled serious trouble for the Genesis account of creation.  

In fact, though, much, much greater trouble for Genesis lay ahead.  I’m going to begin to tell the story of that trouble in this blog.  Before proceeding, though, I want apologize for the long delay since the last installment.  In the course of writing this series, I came to realize that, by providing a little more historical background and detail than first envisioned, I could kill two birds with one stone, and close another gap in most people’s knowledge of astronomy.  We’ve all become used to the stunning photographs provided by the big telescopes of our day, most notably the Hubble Space Telescope.  But have you ever wondered how astronomers actually exploit the crispness of these images to do science; that is, how they use telescopes to answer questions and roll back the boundaries of our ignorance?  The story I’m about to tell provides a very concrete example of one way that astronomers use the power of their telescopes to unlock the secrets of the cosmos.

So let’s get to it.  Encouraged by the initial success of Bessel and his colleagues in the late 1830’s, astronomers spent the better part of the next 60 years trying to measure parallax angles for a vast number of other stars, including some of the brightest in the sky.  Believe it or not, in all that time they managed to obtain reliable angles for only a handful of additional stars, none more than 26 light years away.  The problem was the Earth’s atmosphere, which causes the images of the stars to jump around constantly.  Small thought these jumps are, they prevented astronomers of the time from making precise enough positional determinations to also measure the apparent movement of the stars as the earth travelled from one side of the Sun to the other.   We can only imagine scientists’ frustration with this state of affairs, since their telescopes had long since revealed that the heavens were absolutely teeming with millions upon millions of stars, most too faint to be seen with the naked eye.  Would there never be a way to measure how far away they are?

Clearly, an alternative was needed to the trigonometric parallax method.   When we look up at the night sky, one of the most obvious features of the stars is how much they differ in brightness.  A few, like Sirius, blaze like little beacons.  Others are just barely visible.  On the straightforward assumption that bright stars are closer to us than dim stars, couldn’t astronomers use a star’s brightness to determine its distance?

Mathematically, the answer is a straightforward “yes”!  The relation between the brightness of an object and how far away it is follows a really simple relation known as the inverse square law.  To get a feeling for this law, suppose you took two identical candles, placed one 10 feet away from you and the other 20 feet away from you, and lit them both.  How much brighter would the nearer candle be than the farther candle?

Intuition might suggest that the more distant candle, being twice as far away, would be half as bright.  Not so, however.  The geometry of the situation dictates that exactly four times as much light would reach your eye from the nearer candle than the farther candle, so the farther candle would be only 1/4 as bright.  Note that the denominator of that fraction, 4, is 2 times itself, or 2 squared.  Next, suppose you measure the brightness of the more distant candle after moving it an additional 10 feet away, so it is now 30 feet away from you, or three times as far away as the nearer candle.  Your measurement would reveal that it is only 1/9 as bright (3 squared).  At risk of belaboring the point, if you moved the more distant candle out another 10 feet, making it 40 feet away (4 times the distance of the nearer candle), it would appear only 1/16 as bright (4 squared).  And so on.

Now suppose you had a friend position the second candle instead of yourself, so that you didn’t actually know how far away it was.  Could you use the inverse square law to compute its distance?  Easily!  For example, suppose you measured that candle’s brightness to be only 1/25 the brightness of the nearby candle.  Since 5 squared equals 25, you would know that the more distant candle is five times as far away as the nearer candle, or 50 feet. It’s a classic example of the power of a simple mathematical relation to solve for an important unknown!

The inverse square law applies equally well to stars as to candles.  If two stars shine with the same “intrinsic” (astronomers call it “absolute”) brightness, and one star is four times as far away as the other, the more distant star will be 1/16 as bright.  As long as you know the distance to the nearer star, calculating the distance to the further one is trivial.  

Now, back to the beginning of the 20^th century.  Fired up by the inverse square law, an astronomer of that period might have measured the brightness of a target star that had not yielded a measurable parallax angle (and whose distance was therefore undetermined), and compare that brightness to the brightness of a star of known distance, such as Sirius, which is about 8 light years distant.  Suppose he found that his target star was 1/16 as bright as Sirius.  The inverse square law would tell him that his star was four times as far away, or 32 light years from Earth.

Unfortunately, applying the inverse square law is only that straightforward if the two stars whose brightness is being compared have the same intrinsic brightness, like two identical candles.  In our stellar example, the target star would have to have the same absolute brightness as Sirius.  The problem is, stars do not all shine with equal brightness; they range from thousands of times dimmer than the Sun to a million times brighter.  Is our target star 1/16 as bright as Sirius because it is actually much brighter than Sirius, but also much further away than 32 light years?  Or is it 1/16 as bright because it is the same distance as Sirius (or even closer) but intrinsically much dimmer?  Without additional information about the star, you just can’t tell.

Might there be a way to get around this problem and still utilize the inverse square law?  In the next blog, we’ll find out the answer.

Of Parallax and Paradox

  And the evening and the morning were the third day.

14  And God said, Let there be lights in the firmament of the heaven to divide the day from the night; and let them be for signs, and for seasons, and for days, and years;

15  And let them be for lights in the firmament of the heaven to give light upon the earth; it was so.

16  And God made two great lights; the greater light to rule the day and the lesser light to rule the night; he made the stars also.

17  And God set them in the firmament of the heaven to give light upon the earth,

18  And to rule over the day and over the night, and to divide the light from the darkness; and God saw that it was good.

19  And the evening and the morning were the fourth day.

Genesis, Chapter 1, verses 13-19

Last week, in part two of the current series, I told the story of how astronomer Ole Roemer first discovered that light does not move from one place to another instantaneously, and how he made his initial calculation of the actual speed that light travels.  In retrospect, I should perhaps have given more emphasis to the many additional experiments that have been conducted to measure the speed of light in the centuries since Roemer did it.  These measurements, involving ever-more accurate devices and improved experimental techniques, are the reason that we have such an exact value (299,792.458 kilometers per second) today.  Some discussion of these experiments would have established, beyond a shadow of a doubt, that 299,792.458 kilometers per second is not a “hypothesis” or a “theory” about the behavior of light that is subject to debate, or could be overturned in some future experiment.   299,792. 458 kilometers per second is a concrete fact, as real as the hand in front of your face.

The importance of the fact that light’s speed (physicists call it “c”) is a far cry from infinite will become clear a little later on.  Right now, I want to begin a different topic with a simple question:  In all the times in your life that you’ve been outside at night, and looking up at the planets and the stars, have you ever wondered how, and when, people began to figure out how far away they are?  Determining their distances certainly wasn’t easy.  For the vast majority of the time that we humans have been around, we lacked the right perspective to even frame the question correctly.   That’s because, just like the Sun appears to rotate around the earth each day (an illusion which made it devilishly difficult to understand that it is really the Earth that is rotating), the night sky looks like a two dimensional surface, at a fixed distance from the Earth, with little lights plastered across its surface.  Imprisoned, constrained, and completely fooled by this compelling illusion, the ancients proposed all sorts of colorful beliefs about the night sky, all of which were premised on the assumption that the heavenly lights were all the same fixed distance away.  One of my personal favorites held that a black curtain surrounds the earth, and the stars are holes in the cloth through which the dazzling brilliance of heaven is shining through.

It was the Greeks who started to part the curtain by employing a straightforward mathematical tool called trigonometric parallax.  To get a quick and dirty feeling for the tool without the messy mathematical details, all you need to do is carry out the following simple exercise.   Position yourself directly in front of your television at a comfortable distance away.  Close your left eye.  Raise your index finger of your right hand straight up in the air.  Position your index finger directly in front of, and about six inches away from, your nose.  Make sure your finger is located directly in front of the middle of your television screen. 

Next, without moving your finger, open your left eye and close your right eye simultaneously.  You’ll see your finger “jump” quite a ways to the right, maybe even all the way off your TV screen (if your screen is small enough, and you are far enough away).  Now, repeat the exercise, but extend your arm all the way so that your right index finger is as far as it can possibly get from your nose.  You will still see your finger “jump” when you switch eyes, but the distance covered by the jump will be noticeably reduced, small enough that your finger probably stays well inside the boundary of the TV screen.

The change in the position of your finger with respect to the background TV is simply due to the fact that you are looking at your finger (and the more distant TV screen) from slightly different positions when you switch eyes.  The closer your finger is to your eyes, the greater the difference those two positions will make, and the more your finger will appear to jump against the screen.  This is where the mathematics comes in.  If you know the exact distance between your right eye and your left eye (the two viewing points), and you know exactly how far your finger appeared to move against the TV screen in the background, you can use simple high school trigonometry, invented by the Greeks, to calculate exactly how far your finger is from your eyes.

What’s the take-home message from our little example?  As long as you can observe a foreground object (like your finger) from two separate locations (like your left and right eyes), and you have background objects much further away from you than the foreground object, then by measuring the amount that the foreground object appears to shift against the background, when observed from the two locations, you can recover the crucial third dimension, and determine exactly how far away the foreground object is from you.

In the thousands of years since this “trigonometric parallax” method was discovered, it has been used routinely to solve all kinds of useful problems, like determining how far a ship is from the shore.  Military types used to need that information in order to figure out how to fire their cannons to hit enemy vessels.  Not to be outdone, both the ancient Greeks and the first generation of astronomers to have access to telescopes used trigonometric parallax to calculate of the distance to objects within our own solar system.  For example, at about the same time that Ole Roemer was making his first observations of Io, Jupiter’s moon, Italian astronomer Giovanni Cassini was making careful observations of where the planet Mars was located with respect to nearby background stars from his location in Paris.  Moreover, Cassini had a research assistant make the same measurements from Equatorial Guinea, several thousand kilometers away (see the figure below). Through trigonometric parallax, Cassini determined a distance to Mars that was only 7% off of the currently accepted value, which we get far more directly by bouncing radar signals off the planet and measuring how long they take to return.

Does trigonometric parallax even work as a tool to measure the distance to the stars? Certainly not by placing observers at a known distance from each other on the Earth’s surface, the way Cassini did for Mars.  The shift in the star’s location against a background of more distant stars would be far too tiny to measure.  Every six months, however, the Earth itself moves in its orbit from one side of the Sun to the other, covering about 186 million miles in the process.  Perhaps that was a displacement large enough for the trigonometric parallax method to work?  Starting around the beginning of the 18^th century, astronomers began to pick candidate stars and, with the help of telescopes, note their exact positions, relative to other stars in their vicinity on, say, Dec 21^st, and then again on June 21^st, six months later.  The method is illustrated in the figure below.  If one of the target stars was observed to move against the other stars in its vicinity, the movement had to be due to the fact that the foreground star was being observed from two different locations, like it was being observed from two eyes, except the two locations were separated by those 186 million miles!  If the size of the shift in position could be measured reliably, astronomers would have all the information needed to calculate the distance to the foreground object (the target star).

Simple, right?  Well, yeah, except that for the longest time, no matter what star they selected as the target, the poor astronomers couldn’t measure any shift.  Luckily for us all (all, that is, except those who cling to the literal truth of Genesis) failure was not an option, and by the early 19^th century, several astronomers were competing to be the first to measure stellar parallaxes and compute stellar distances.  Finally, in 1838, an anal German scientist (is there any other sort?) named Friedrich Bessel won the race, and reported a reliable parallax shift for 61 Cygni (a relatively unassuming star in the constellation Cygnus).  Bessel had had good reason to suspect that this particular star might be a relatively near neighbor to the Sun (how Bessel made that determination is interesting in its own right, but beyond the scope of this blog), and was therefore a good candidate to reveal a parallax.  That parallax was exceedingly tiny, though, so small that when Bessel computed the distance to 61 Cygni, it came out to a jaw-dropping 52 trillion miles.

Suddenly, everything clicked into place.  As more stars had their distances determined, it became clear that the trigonometric parallax method had failed for so long simply because the stars are so mind-numbingly distant, which means that the amount they appear to shift was exceedingly tiny.  Although other stars were discovered to be closer than 61 Cygni, none were found any closer than Alpha Centauri, at 26 trillion miles away.  

Time to connect some dots.  At a speed of almost 300,000 kilometers per second, how long does it take light to cross the space between the stars and reach our eyes and our telescopes?  In the case of even the closest star, Alpha Centauri, the answer is 4.2 years. In the case of 61 Cygni, the answer is closer to 10 light years.  For other familiar stars, like Vega, we’re talking more like 26 years.

According to the Genesis version of creation, these stars all popped into existence in the course of a single day, the fourth after creation, and were lighting up the night sky by the time the fourth day came to an end.  But if we take into account the speed of light, and the distance of these stars from the Earth, this is flatly impossible.  On the assumption that the stars were approximately the same distance from the Earth 6000 years ago as they were when Bessel and his colleagues first measured their parallaxes (and, to a first order of approximation, that is the case), then their light had just gotten started on its journey to Earth on the day they were created, and would not have reached the Earth for years.  At risk of belaboring this point, the night sky would have been completely bereft of stars for the first 4.2 years, and then one single, solidarity point of light, the star we now call Alpha Centauri, would have winked on.  It would have taken the entire lifetime of Adam and Eve, for instance, for all the familiar stars in our sky to gradually become visible.

All right, you’re saying.  God has a lot of tricks up His sleeve.  Maybe he got around the pesky little speed-of-light problem by pulling a fast one on us.  Maybe, when He created the stars that would be visible to Adam and Eve in the night sky, He initially placed them all well inside the confines of our own solar system, close enough that they would all be visible on the evening of the fourth day (after all, he had up to 24 hours of wiggle room, so he could put them as far as 16 billion miles out in space, way past the orbit of Pluto, and their light would still have reached the earth before His deadline).   Then, maybe God employed some rather adroit stellar dynamics to whisk these stars out of the solar system fast enough that they would reach their present gargantuan distances in time for Bessel and his colleagues to measure them, 6000 years later. 

Fair enough.  After all, God is omnipotent, so there is really nothing beyond his power to accomplish if He sets his mind to it.  But even this incredible kluge cannot save Genesis, because, embedded in the speed of light and the distances to celestial objects lurks a far more profound challenge to the story.   That challenge will be the subject of the next blog.  Until then, would anybody like to try and trump me and hazard a guess as to what it is?

Science and Religion at the Speed of Light

In the last blog, I promised to demolish the Genesis account of creation without referencing Darwin, evolution, or anything to do with Earth’s geology.  Instead, I’m going to build my case with ironclad facts from the fields of physics and astronomy, facts that have been established over the course of hundreds of years of painstaking inquiry into the nature of physical reality. 

Although no one knew it at the time, Genesis began to unravel the very first time somebody looked at the planet Jupiter through a telescope.  As most of you know, the person in question was Galileo, and the time was the beginning of the 17^th century.  To his great astonishment, Galileo observed four points of light surrounding the giant planet.  Observing them over time, he noted that the positions of the lights changed in ways that made it obvious that they were satellites, orbiting Jupiter in the same way that the planets orbit the Sun.

One of these lights, Jupiter’s moon Io, is so close to Jupiter that it completes a full orbit in only a couple of days, going behind Jupiter for a brief period each time (in astronomy-speak, Jupiter “occults” Io).  Later on in the 17th century, the prominent Danish astronomer Ole Roemer systematically recorded the timing of these occultations over an extended period stretching from 1671 to 1677.   Combining his observations with those of some of his contemporaries, Roemer discovered a remarkably systematic pattern: the time between occultations gets steadily shorter as the Earth’s own orbital motion brings us closer to Jupiter, and then lengthens again as the Earth moves farther away.  Reporting his results to the French Academy of Sciences, Roemer hypothesized that

This… appears to be due to light taking some time to reach us from the satellite; light seems to take about ten to eleven minutes [to cross] a distance equal to the half-diameter of the terrestrial orbit

Clever fellow that he was, Roemer combined this time difference with early estimates of the “half-diameter of the terrestrial orbit” (the distance from the Earth to the Sun, from which he could easily calculate the difference in distance between the Earth and Jupiter when they are closest together compared to when they are furthest apart) to compute the speed of light for the first time (prior to that point, many prominent scientists, Newton included, believed the speed of light was infinite). 

The value Roemer obtained, about 211, 000 kilometers per second, is considerably lower than the currently accepted value of 299,792.458 kilometers per second.  That’s because the radius of the Earth’s orbit wasn’t yet known with any precision in his time.  Still, Roemer’s calculation was in the right ballpark, and the realization that the speed of light had a fixed value, instead of being either immeasurably high or infinite, marked a major advance in the history of science and our understanding of the natural world.  For example, we’ve already seen how fundamental a role the finite speed of light plays in generating time dilation effects.  In subsequent blogs, we’ll discover just how big a nail the speed of light was to drive in the coffin of the biblical story of creation.  But first, we have to identify another important nail, in the form of the distance between the stars and us.  That is the topic of the next blog.

In the beginning was the Word

 

The Holy Bible was written by men divinely inspired and is God's revelation of Himself to man. It is a perfect treasure of divine instruction. It has God for its author, salvation for its end, and truth, without any mixture of error, for its matter. Therefore, all Scripture is totally true and trustworthy. – from the Basic Beliefs of the Southern Baptist Church, currently 16 million members strong

At the core of most major religions is the belief that the universe has not existed forever.  Instead, it was created by a higher power at some specific point in the past, usually to provide a backdrop or platform for humanity to inhabit. Interestingly, arguably the most profound scientific discovery of the 20^th century was that the Universe has, in fact, not been around forever.  About 13.7 billion years ago, by current best estimates, the whole enchilada started out as an almost infinitely hot and infinitely dense speck, so tiny that even our most powerful microscopes couldn’t have seen it.  From there, the speck started to expand and cool, a process that is still going on today.  This “big bang” account leaves the question of how (and, if you insist, why) the universe came into being completely open.  The Catholic Church, for example, sees in the big bang the undeniable handiwork of God the Creator.

The church may be right.  In the absence of any evidence one way or the other, divine intervention has just much right to a seat at the table as any other conjecture.  Thus, in concert with those of a religious persuasion, I’m quite open to the possibility that the Universe had a creator.  However, there is one particular religious belief concerning creation that I could not disagree more violently with: the specific details of the creation account as described in the Old Testament. Actually, to say I “disagree with” the biblical version of creation doesn’t do my position justice.  The Genesis version of the Universe’s creation can’t possibly be correct.  It’s just flat-out wrong. It’s untrue.  The sooner that all religions and denominations embrace the Catholic notion that Genesis should be taken figuratively, not literally, the better off all of us will be, believers and non-believers alike. 

This embrace cannot come fast enough for me. As recently as 2008, a Gallup poll found that fully 44% of US adults agreed with the statement "God created human beings pretty much in their present form at one time within the last 10,000 years or so”.   We can assume that a similar percentage would have agreed with the statement “God created the heavens and the Earth sometime in the last 10,000 years” as well, had this question also been asked.

So what does Genesis actually say?  Very briefly, Chapter 1 asserts that the heavens, the earth, and all living creatures, including the first humans, were created in the space of six days.  Assuming that the subsequent course of human history, as laid out in the Bible, proceeded uninterrupted from that week, various Biblical scholars have computed the time that has elapsed since that monumental week as about 6000 years. 

In this latest series of blogs, I’m going to confront this Biblical account of creation head on.  But I’m not going to go about it the standard way, which is to champion Darwinian evolutionary theory over the Genesis story of how humans came to be, or to lob geological arguments at the Young Earth Creation (YEC) movement, whose members assert that most of the geological evidence for an old Earth is instead the product of a relatively recent event - Noah’s flood.  These conventional ways of framing the issue might well be futile anyway.  In the words of the YECs themselves,

“We further deny that scientific hypotheses about Earth history may properly be used to overturn the teaching of Scripture on creation and the flood”.

So what kind of argument am I going to mount instead? I’m afraid you’ll have to check out the next blog to begin to find out!